The granocentric model takes a microscopic approach, creating the statistics of a single cell – a central particles and its contacting and neighboring spheres as well as the cell volume. (contacting spheres provide mechanical stability; cells are creating by tessellating space with a navigation map, assigning volume to the sphere whosesurface is nearest; two sphere are neighboring if they share a cell wall). The model creates cells by choosing contacting and neighboring particles independently at random until the available solid angle around the central particle is filled; it is an increasing random walk to a threshold. Each surrounding particle contributes the volume of a cone subtended by its solid angle with a hyperbolic cap given by the navigation map. By changing the three model parameters, the average number of contacts, neighbors and the packing fraction can be modified, reproducing a large range of experimentally observed packings. Pairs of cells generated by repeating the method of cell creation on one of the neighboring particles of the original cell will model experimentally observed spatial correlations.
Working under the hypothesis that packings occupying the same total volume have the same macroscopic properties, Edwards’ statistical mechanics framework proposed to describe a randomly packed state using thermodynamic quantities that are analogous to those used in thermal systems: the system volume replaces the energy, and the compactivity replaces the temperature. While the Gibbs entropy is not accessible using the granocentric model, its approximation by the Boltzmann entropy can be readily calculated from the probability density of a single cell’s volume. The entropy can be related to the compactivity as the inverse of the derivative of the entropy with respect to the average cell volume. The granocentric model captures our physical intuition about compactivity. States with lower density have higher compactivity, and therefore a greater ability to compactify further. Similarly states with fewer contacts have higher compactivity than states with the same density and more contacts.
[pdf] K. Newhall, I. Jorjadze, E. Vanden-Eijnden, and J. Brujic (2011) A statistical mechanics framework captures the packing of monodisperse particles, Soft Matter, 7, 11518-11525
I simplified the model in order to derive the observed size-topology relationships in not only granular material, but biological cells and foams as well, such as that between neighbor number and cell size. Rather than creating cells with the stochastic process, I created a `mean-field’ cell by surrounding a central particle with contacting averaged-sized particles for polydisperse packings or with same-sized particles placed a characteristic distance away for monodisperse packings. This decouples the effects of size-disorder and positional-disorder and reveals that foam and polydisperse granular materials are dominated by size-disorder: a larger central particle for a cell leads to more neighbors and larger volume. On the other hand, biological tissues and randomly packed monodisperse disks are dominated by positional-disorder: placing neighbors further away allows for more neighbors to fit in, and larger cell sizes.
[pdf] K. Newhall, L. Pontani, I. Jorjadze, S. Hilgenfeldt, J. Brujic (2012) Size-topology relations in packings of grains, emulsions, foams and biological cells, PRL, 108, 268001
Polarization Switching of Solitons
Soliton solutions to the Maxwell-Bloch equation (describing the resonant interaction between classical electromagnetic fields and materials described by quantum mechanics) explain the experimentally observed self-induced transparency phenomena. In a three-level system with degenerate ground levels and constant initial lower-level populations, the resulting soliton pulse is non-trivial, as both the light pulse’s shape and velocity change before reaching one of its two asymptotically stationary states. I am interested in the initially randomly prepared material (modeled by white noise) and relating the characteristics of the polarization switching to statistics of Brownian motion and first passage times.
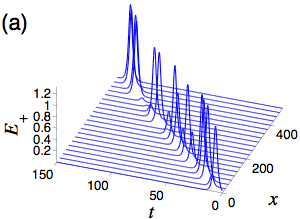
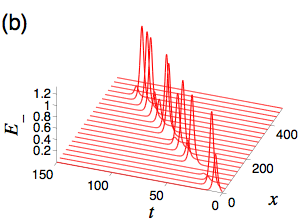
In a resonant interaction, light of a specific wavelength excites a particular electron transition between two atomic energy levels in an active optical medium such as a rarefied gas or a crystal. An important special active medium with a doubly degenerate ground level and an excited level is referred to as the Lambda-configuration medium. For example, it can be prepared to slow down light propagation speed to a fraction of its value in a vacuum. The two types of atomic transitions in such a medium are stimulated by and emit light of two opposite circular polarizations. The dynamics of a soliton pulse of light depend non-trivially on the initial preparation of the material; changing both its shape and velocity before reaching one of its two asymptotically stationary polarization states. Using the Maxwell-Bloch system to model the light-material interaction in a randomly prepared material results in a completely integrable, yet stochastic system.
The statistics of the electric-field polarization ellipse at a given point along the medium are derived from the inverse scattering method obtained solution for the two electric fields. The orientation angle of the ellipse undergoes Brownian motion with a drift equal to the initial difference between the average occupations of the two lower levels. For non-zero drift, Brownian motion tends towards plus or minus infinity resulting in a polarization orientation, eta, of plus or minus pi/4 indicating either right or left circularly polarized light is the asymptotically stable state. Solving the first passage time problem of eta to a small neighborhood of plus or minus pi/4 results in the statistics for the distance the light pulse travels before reaching its finial state. For zero drift (equal initial occupations on average), Brownian motion will forever return to zero, and also take long excursions from zero, resulting in a polarization orientation that stays in one of the two circular polarizations for a long time, but then switches to the other and vice versa. The distributions of the distances between the polarization switches along the optical medium and of the switch lengths are obtained through appropriate first passage time calculations. Currently, I am working to understand the role of tunneling between the ground states, whose predominate effect is to alter the asymptotically stable polarization orientations. This involves computing the analytical solutions for the material as well as the electric field using the dressing method.
[pdf] K. Newhall, E. Atkins, P. Kramer, G. Kovacic, I. Gabitov (2013) Random polarization dynamics in a resonant optical medium, Optics Letters, Vol. 38, No. 6, pp. 893-895
For the case of initial coherence in the material, corresponding to the forbidden transition between the two lower energy levels, we find two polarization states that are stationary. They are not the purely right- and left-circularly polarized solitons (plus or minus pi/4), as in the case of zero initial coherence, but rather two mixed, elliptically polarized, states. These polarization states, of which only one is asymptotically stable, depend on both the initial population levels of the lower states and the coherence value. We also find the existence of superluminal soliton propagation, but through numerical simulations show this solution to be unstable, and therefore likely not realizable physically.
[pdf] K. Newhall, G. Kovačič, I. Gabitov (2020, accepted 2018) Polarization dynamics in a resonant optical medium with initial coherence between degenerate states, Discrete Contin. Dyn. Syst. Ser. S, Vol. 13, No. 8, pp. 2285-2301
Characterizing Stochastic Synchrony
The stochastically-driven, current-based, Integrate-and-Fire (IF) neuronal network model provides an ideal situation to study the underlying mechanism responsible for synchrony in the presence of noisy input. For my Thesis, I characterized the competition between the desynchronizing, noisy input, which drives each neuronal voltage and the synchronizing instantaneous pulse-coupling between the neurons in the network in terms of single neuron statistics. I have proceeded to modify this bridge between the single neuronal descriptors and the global characterization of synchrony by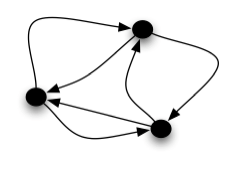
including the connectivity statistics of complex networks into the description of synchrony. I worked to understand the role of inhibitory neurons in the distribution of the number of neurons participating in a synchronous burst, one piece required for adapting population based simulation methods to non-homogeneous dynamical regimes.
The most basic, as well as most pronounced, type of synchrony I have observed consistently in a model of excitatory neuron networks is that of “cascading total firing events,” during which all neurons fire at once in random time-intervals that have a well defined mean. For the idealized, all-to-all-coupled network (in which each neuron sends equal-strength spikes to every other neuron when it fires), I have developed analytical theories describing (i) the probability cascading total firing events are seen in succession, and (ii) the distribution of time between such two events. The time between two cascading total firing events is precisely equal to the time it took the first of all the model neurons to fire since the previous total firing event. I have computed this time as the minimum of the random times when each neuron would spike if
not coupled. I have derived its pdf from the single neuron spike time, described by a first-passage-time problem whose solution I found using a Fokker-Planck equation for a defective voltage pdf. For the probability that cascading total firing events are seen in succession, I have calculated the probability that earlier spikes in the cascade cause more neurons to fire with a combinatorial “balls-in-bins” method, based on the random time the first neuron fired since the previous cascading total firing event, and the single neuron voltage distribution at this time.
[pdf] K. Newhall, G. Kovacic, P. Kramer, A. Rangan, and D. Cai (2010) Cascade-Induced Synchrony in Stochastically-Driven Neuronal Networks, Phys. Rev. E., 82, 041903.
[pdf] K. Newhall, G. Kovacic, P. Kramer, D. Zhou, A. Rangan, and D. Cai (2010) Dynamics of Current-Based, Poisson Driven, Integrate-and-Fire Neuronal Networks, Comm. in Math. Sci., Vol. 8, No. 2, pp. 541-600.
With the addition of a population of inhibitory neurons, synchrony becomes instantaneous bursts of firing (not necessarily including the entire network) separated by periods of seemingly homogeneous firing. These two regimes of firing can be explained by the cascading firing mechanism alone. Starting from a distribution for each population of neuronal voltages at the time the first excitatory neuron fires I calculated the number of neurons participating in a cascading firing event in terms of the exit time of a 2D stochastic process over a moving boundary. Fluctuations in the positions of the neuronal voltages near threshold create firing events with only one or two neurons while the mean of the processes control the average size of larger events.
[pdf] J. Zhang, K. Newhall, D. Zhou, A. Rangan (2013) Distribution of correlated spiking events in a population-based approach for Integrate-and-Fire networks, J. Comput. Neurosci., published online
It is known that real neuronal systems cannot be all-to-all connected, but rather have a complex network topology. In these systems, there are two independent sources of noise effecting the synchrony, one from the network connections and one from the voltage dynamics. To account for their interaction in networks of excitatory neurons, I have extended the theory for the probability of cascading total firing events to occur in succession to accounts for different network topologies as well as synaptic failure (i.e., the failure of a neuron to register an incoming spike). For complex network topologies, I looked at local network motifs around the firing neuron initiating the cascade, and developed a second order theory with a detailed analytical calculation depending on a new characterization of clustering that improves the usual tree-based theory. This theory relies on the assumption that once three neurons fire, the cascade continues throughout the network with very high probability. In order to relax this assumption, I am also currently modifying existing theories for percolation on networks, such as those of Newman and Gleeson, to account for the voltage dynamics of neurons. This will help illuminate the interplay between the network and dynamical effects, and in what regimes they dominate the synchronous dynamics.
K. Newhall, M. Shkarayev, P. Kramer, G. Kovačič, and D. Cai (2015) Synchrony in stochastically driven neuronal networks with complex topologies, Phys. Rev. E 91, 052806

University Operator: (919) 962-2211 | © 2024 The University of North Carolina at Chapel Hill |